|
Overline
An overline, overscore, or overbar, is a typographical feature of a horizontal and vertical, horizontal line drawn immediately above the text. In old mathematical notation, an overline was called a ''vinculum (symbol), vinculum'', a notation for grouping symbols which is expressed in modern notation by parentheses, though it persists for symbols under a radical sign. The original use in Ancient Greek was to indicate compositions of Greek alphabet, Greek letters as Greek numerals. In Latin, it indicates Roman numerals multiplied by a thousand and it forms medieval abbreviations (sigla). Marking one or more words with a continuous line above the characters is sometimes called ''overstriking'', though overstriking generally refers to printing one character on top of an already-printed character. An overline, that is, a single line above a chunk of text, should not be confused with the macron (diacritic), macron, a diacritical mark placed above (or sometimes below) ''individual'' le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vinculum (symbol)
\overline = 0. \overline Y = \overline \sqrt[n] a-\overline = a − (b + c) bracketing function Vinculum usage A vinculum () is a horizontal line used in mathematical notation for various purposes. It may be placed as an ''overline'' or ''underline'' above or below a mathematical expression to group the expression's elements. Historically, vincula were extensively used to group items together, especially in written mathematics, but in modern mathematics its use for this purpose has almost entirely been replaced by the use of parentheses. It was also used to Roman numerals#Vinculum, mark Roman numerals whose values are multiplied by 1,000. Today, however, the common usage of a vinculum to indicate the repetend of a repeating decimal is a significant exception and reflects the original usage. History The vinculum, in its general use, was introduced by Frans van Schooten in 1646 as he edited the works of François Viète (who had himself not used this notation). However, ea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Macron (diacritic)
A macron ( ) is a diacritical mark: it is a straight bar placed above a letter, usually a vowel. Its name derives from Ancient Greek (''makrón'') 'long' because it was originally used to mark long or heavy syllables in Greco-Roman metrics. It now more often marks a long vowel. In the International Phonetic Alphabet, the macron is used to indicate a mid-tone; the sign for a long vowel is instead a modified triangular colon . The opposite is the breve , which marks a short or light syllable or a short vowel. Uses Syllable weight In Greco-Roman metrics and in the description of the metrics of other literatures, the macron was introduced and is still widely used in dictionaries and educational materials to mark a long (heavy) syllable. Even relatively recent classical Greek and Latin dictionaries are still concerned with indicating only the length (weight) of syllables; that is why most still do not indicate the length of vowels in syllables that are otherwise metrica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diacritical Mark
A diacritic (also diacritical mark, diacritical point, diacritical sign, or accent) is a glyph added to a letter or to a basic glyph. The term derives from the Ancient Greek (, "distinguishing"), from (, "to distinguish"). The word ''diacritic'' is a noun, though it is sometimes used in an attributive sense, whereas ''diacritical'' is only an adjective. Some diacritics, such as the acute , grave , and circumflex (all shown above an 'o'), are often called ''accents''. Diacritics may appear above or below a letter or in some other position such as within the letter or between two letters. The main use of diacritics in Latin script is to change the sound-values of the letters to which they are added. Historically, English has used the diaeresis diacritic to indicate the correct pronunciation of ambiguous words, such as "coöperate", without which the letter sequence could be misinterpreted to be pronounced . Other examples are the acute and grave accents, which can indicate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Macron (symbol)
A macron ( ) is a diacritical mark: it is a straight bar placed above a letter, usually a vowel. Its name derives from Ancient Greek (''makrón'') 'long' because it was originally used to mark long or heavy syllables in Greco-Roman metrics. It now more often marks a long vowel. In the International Phonetic Alphabet, the macron is used to indicate a mid-tone; the sign for a long vowel is instead a modified triangular colon . The opposite is the breve , which marks a short or light syllable or a short vowel. Uses Syllable weight In Greco-Roman metrics and in the description of the metrics of other literatures, the macron was introduced and is still widely used in dictionaries and educational materials to mark a long (heavy) syllable. Even relatively recent classical Greek and Latin dictionaries are still concerned with indicating only the length (weight) of syllables; that is why most still do not indicate the length of vowels in syllables that are otherwise metrical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Notation
Mathematical notation consists of using glossary of mathematical symbols, symbols for representing operation (mathematics), operations, unspecified numbers, relation (mathematics), relations, and any other mathematical objects and assembling them into expression (mathematics), expressions and formulas. Mathematical notation is widely used in mathematics, science, and engineering for representing complex concepts and property (philosophy), properties in a concise, unambiguous, and accurate way. For example, the physicist Albert Einstein's formula E=mc^2 is the quantitative representation in mathematical notation of mass–energy equivalence. Mathematical notation was first introduced by François Viète at the end of the 16th century and largely expanded during the 17th and 18th centuries by René Descartes, Isaac Newton, Gottfried Wilhelm Leibniz, and overall Leonhard Euler. Symbols and typeface The use of many symbols is the basis of mathematical notation. They play a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medical Prescription
A prescription, often abbreviated or Rx, is a formal communication from physicians or other registered healthcare professionals to a pharmacist, authorizing them to dispense a specific prescription drug for a specific patient. Historically, it was a physician's instruction to an apothecary listing the materials to be compounded into a treatmentthe symbol (a capital letter R, crossed to indicate abbreviation) comes from the first word of a medieval prescription, Latin (), that gave the list of the materials to be compounded. Format and definition For a communication to be accepted as a legal medical prescription, it needs to be filed by a qualified dentist, advanced practice nurse, physician, or veterinarian, for whom the medication prescribed is within their scope of practice to prescribe. This is regardless of whether the prescription includes prescription drugs, controlled substances, or over-the-counter treatments. Prescriptions may be entered into an electron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Theory
Set theory is the branch of mathematical logic that studies Set (mathematics), sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathematics – is mostly concerned with those that are relevant to mathematics as a whole. The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of ''naive set theory''. After the discovery of Paradoxes of set theory, paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied. Set the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Survival Function
The survival function is a function that gives the probability that a patient, device, or other object of interest will survive past a certain time. The survival function is also known as the survivor function or reliability function. The term ''reliability function'' is common in engineering while the term ''survival function'' is used in a broader range of applications, including human mortality. The survival function is the complementary cumulative distribution function of the lifetime. Sometimes complementary cumulative distribution functions are called survival functions in general. Definition Let the lifetime T be a continuous random variable describing the time to failure. If T has cumulative distribution function F(t) and probability density function f(t) on the interval [0,\infty), then the ''survival function'' or ''reliability function'' is: S(t) = P(T > t) = 1-F(t) = 1 - \int_0^t f(u)\,du Examples of survival functions The graphs below show examples of hypot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample Mean
The sample mean (sample average) or empirical mean (empirical average), and the sample covariance or empirical covariance are statistics computed from a sample of data on one or more random variables. The sample mean is the average value (or mean value) of a sample of numbers taken from a larger population of numbers, where "population" indicates not number of people but the entirety of relevant data, whether collected or not. A sample of 40 companies' sales from the Fortune 500 might be used for convenience instead of looking at the population, all 500 companies' sales. The sample mean is used as an estimator for the population mean, the average value in the entire population, where the estimate is more likely to be close to the population mean if the sample is large and representative. The reliability of the sample mean is estimated using the standard error, which in turn is calculated using the variance of the sample. If the sample is random, the standard error falls with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Repeating Decimal
A repeating decimal or recurring decimal is a decimal representation of a number whose digits are eventually periodic (that is, after some place, the same sequence of digits is repeated forever); if this sequence consists only of zeros (that is if there is only a finite number of nonzero digits), the decimal is said to be ''terminating'', and is not considered as repeating. It can be shown that a number is rational if and only if its decimal representation is repeating or terminating. For example, the decimal representation of becomes periodic just after the decimal point, repeating the single digit "3" forever, i.e. 0.333.... A more complicated example is , whose decimal becomes periodic at the ''second'' digit following the decimal point and then repeats the sequence "144" forever, i.e. 5.8144144144.... Another example of this is , which becomes periodic after the decimal point, repeating the 13-digit pattern "1886792452830" forever, i.e. 11.18867924528301886792452830.... ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
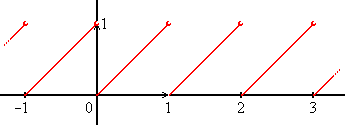
Fractional Part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. The latter is defined as the largest integer not greater than , called ''floor'' of or \lfloor x\rfloor. Then, the fractional part can be formulated as a difference: :\operatorname (x)=x - \lfloor x \rfloor,\; x > 0. The fractional part of logarithms, specifically, is also known as the mantissa; by contrast with the mantissa, the integral part of a logarithm is called its ''characteristic''. The word ''mantissa'' was introduced by Henry Briggs. For a positive number written in a conventional positional numeral system (such as binary or decimal), its fractional part hence corresponds to the digits appearing after the radix point, such as the decimal point in English. The result is a real number in the half-open interval x, -\lfloor , x, \rfloor , or by the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |